Spin representation

Is a particular case of projective representation for the groups $SO(n,m)$ (special orthogonal group with any signature).

Given the group $SO(n,m)$, we can consider the spin group $Spin(n,m)$. Given a representation of $Spin(n,m)$, it may happen that "it descends" to a representation of $SO(n,m)$:

in case that $\rho(A)=\rho(B)$ for $\pi(A)=\pi(B)$. In this case, the representation of $Spin(n,m)$ doesn't provide further information than a usual representation of $S(n,m)$. But, in case that "it doesn't descend", we can consider a lift $h:SO(n,m)\to Spin(n,m)$ to create the map $\tilde{\rho}=\rho \circ h$, which is a projective representation of $SO(n,m)$. In effect, for $g,g'\in SO(n,m)$

since $\pi\circ h=id$:

and then $h(g)h(g')=c(g,g') h(gg')$.

Example. $Spin(3)=SU(2)$ has a representation as 2x2 complex matrices. And this representation can be used to create a spin-representation of $SO(3)$. In some contexts, it is said that that $SO(3)$ has a spin-1 representation, the orthogonal matrices, and a spin-1/2 representation, the special unitary 2x2 matrices. Even if we have different lifts from $SO(3)$ to $Spin(3)$, all the corresponding spin representations are equivalent (I have read that in wikipedia

To think:

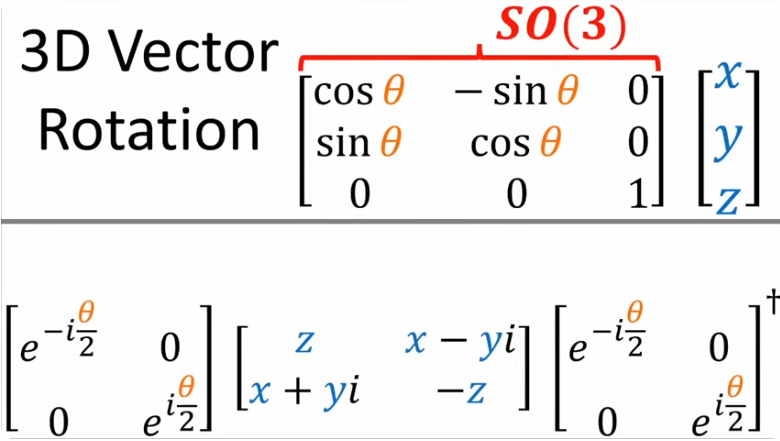
Also related to relation SO(3) and SU(2).

Also, to see the relation between the spin representation and the vector representation of $SO(3)$: see this.

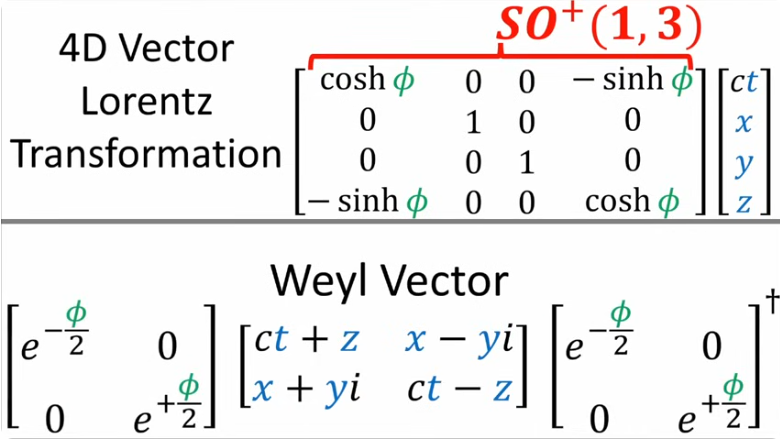
Example. $Spin(1,3)=SL(2,\mathbb C)$ provides two inequivalent spin-representations for $SO(1,3)$. There are two different lifts from $SO(1,3)$ to its double cover $Spin(1,3)$, and I guess it can be shown that there is no isomorphism between the resulting spin representations.

To think

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es